International Mathematics Competition
for University Students
2019

IMC2019: Day 2, Problem 10

Problem 10. \(\displaystyle 2019\) points are chosen at random, independently, and distributed uniformly in the unit disc \(\displaystyle \{(x,y)\in\RR^2\colon x^2+y^2\leq 1\}\). Let \(\displaystyle C\) be the convex hull of the chosen points. Which probability is larger: that \(\displaystyle C\) is a polygon with three vertices, or a polygon with four vertices?

Proposed by Fedor Petrov, St. Petersburg State University

Solution. We will show that the quadrilateral has larger probability.

Let \(\displaystyle \mathcal{D}=\{(x,y)\in\RR^2\colon x^2+y^2\leq 1\}\). Denote the random points by \(\displaystyle X_1,\ldots,X_{2019}\) and let

\(\displaystyle \begin{align*} p &= P\big(\text{\(\displaystyle C\) is a triangle with vertices \(\displaystyle X_1,X_2,X_3\)} \big),\\ q &= P\big(\text{\(\displaystyle C\) is a convex quadrilateral with vertices \(\displaystyle X_1,X_2,X_3,X_4\)} \big). \end{align*} \)

By symmetry we have \(\displaystyle P\big(C\, \text{is a triangle}\big)=\binom{2019}{3} p\), \(\displaystyle P\big(C\, \text{is a quadrilateral}\big)=\binom{2019}{4} q\) and we need to prove that \(\displaystyle \binom{2019}{4} q>\binom{2019}{3} p\), or equivalently \(\displaystyle p<\frac{2016}4 q=504 q\).

Note that \(\displaystyle p\) is the average over \(\displaystyle X_1,X_2,X_3\) of the following expression:

\(\displaystyle u(X_1,X_2,X_3)=P\big(X_4\in \triangle X_1X_2X_3\big)\cdot P\big(X_5, X_6, \ldots, X_{2019}\in \triangle X_1X_2X_3\big), \)

and \(\displaystyle q\) is not less than the average over \(\displaystyle X_1,X_2,X_3\) of

\(\displaystyle v(X_1,X_2,X_3)=P\big(X_1,X_2,X_3,X_4 \,\text{form a convex quad.} \big)\cdot P\big(X_5, X_6, \ldots, X_{2019}\in \triangle X_1X_2X_3)\big). \)

Thus it suffices to prove that \(\displaystyle u(X_1,X_2,X_3)\leq 500 v(X_1,X_2,X_3)\) for all \(\displaystyle X_1,X_2,X_3\). It reads as \(\displaystyle \mathrm{area} (\triangle X_1X_2X_3)\leq 500 \mathrm{area}(\Omega)\), where \(\displaystyle \Omega=\{Y:X_1,X_2,X_3,Y \,\text{form a convex quadrilateral}\}\).

Assume the contrary, i.e., \(\displaystyle \mathrm{area}(\triangle X_1X_2X_3)> 500 \mathrm{area}(\Omega)\).

Let the lines \(\displaystyle X_1X_2\), \(\displaystyle X_1X_3\), \(\displaystyle X_2X_3\) meet the boundary of \(\displaystyle \mathcal{D}\) at \(\displaystyle A_1,A_2,A_3,B_1,B_2,B_3\); these lines divide \(\displaystyle \mathcal{D}\) into \(\displaystyle 7\) regions as shown in the picture; \(\displaystyle \Omega=\mathcal{D}_4\cup\mathcal{D}_5\cup\mathcal{D}_6\).

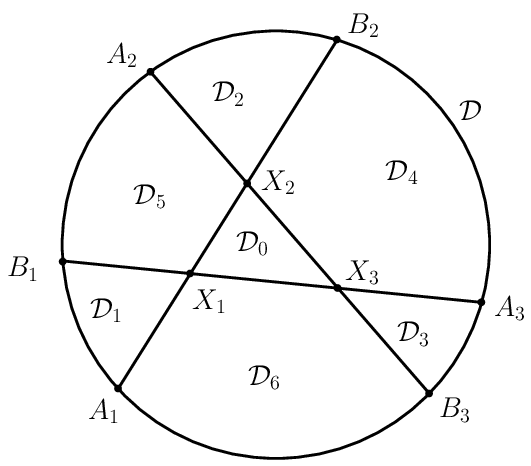
By our indirect assumption,

\(\displaystyle \mathrm{area}(\mathcal{D}_4) + \mathrm{area}(\mathcal{D}_5) + \mathrm{area}(\mathcal{D}_6) = \mathrm{area}(\Omega) < \frac1{500} \mathrm{area}(\mathcal{D}_0) < \frac1{500} \mathrm{area}(\mathcal{D}) = \frac\pi{500}. \)

From \(\displaystyle \triangle X_1X_3B_3\subset \Omega\) we get \(\displaystyle X_3B_3/X_3X_2=\mathrm{area}(\triangle X_1X_3B_3)/\mathrm{area}(\triangle X_1X_2X_3)<1/500\), so \(\displaystyle X_3B_3<\frac1{500}{X_2X_3}<\frac1{250}\). Similarly, the lengths segments \(\displaystyle A_1X_1,B_1X_1,A_2X_2,B_2X_2,A_3X_2\) are less than \(\displaystyle \frac1{250}\).

The regions \(\displaystyle \mathcal{D}_1,\mathcal{D}_2,\mathcal{D}_3\) can be covered by disks with radius \(\displaystyle \frac1{250}\), so

\(\displaystyle \mathrm{area}(\mathcal{D}_1)+\mathrm{area}(\mathcal{D}_2)+\mathrm{area}(\mathcal{D}_3) < 3\cdot \frac{\pi}{250^2}. \)

Finally, it is well-known that the area of any triangle inside the unit disk is at most \(\displaystyle \frac{3\sqrt3}{4}\), so

\(\displaystyle \mathrm{area}(\mathcal{D}_0) \le \frac{3\sqrt3}4. \)

But then

\(\displaystyle \sum_{i=0}^6 \mathrm{area}(\mathcal{D}_i) < \frac{3\sqrt3}4 + 3\cdot \frac{\pi}{250^2} + \frac\pi{500} < \mathrm{area}(\mathcal{D}), \)

contradiction.