International Mathematics Competition
for University Students
2016

IMC2016: Day 2, Problem 8

8. Let $n$ be a positive integer, and denote by $\mathbb{Z}_n$ the ring of integers modulo $n$. Suppose that there exists a function $f:\mathbb{Z}_n\to\mathbb{Z}_n$ satisfying the following three properties:

(i) $f(x)\neq x$,

(ii) $f(f(x))=x$,

(iii) $f(f(f(x+1)+1)+1)=x$ for all $x\in\mathbb{Z}_n$.

Prove that $n\equiv 2 \pmod4$.

Proposed by Ander Lamaison Vidarte, Berlin Mathematical School, Germany

Solution. From property (ii) we can see that $f$ is surjective, so $f$ is a permutation of the elements in $\mathbb{Z}_n$, and its order is at most $2$. Therefore, the permutation $f$ is the product of disjoint transpositions of the form $\big(x,f(x)\big)$. Property (i) yields that this permutation has no fixed point, so $n$ is be even, and the number of transpositions is precisely $n/2$.

Consider the permutation $g(x)=f(x+1)$. If $g$ was odd then $g\circ g\circ g$ also would be odd. But property (iii) constraints that $g\circ g\circ g$ is the identity which is even. So $g$ cannot be odd; $g$ must be even. The cyclic permutation $h(x)=x-1$ has order $n$, an even number, so $h$ is odd. Then $f(x)=g\circ h$ is odd. Since $f$ is the product of $n/2$ transpositions, this shows that $n/2$ must be odd, so $n\equiv 2\pmod4$.

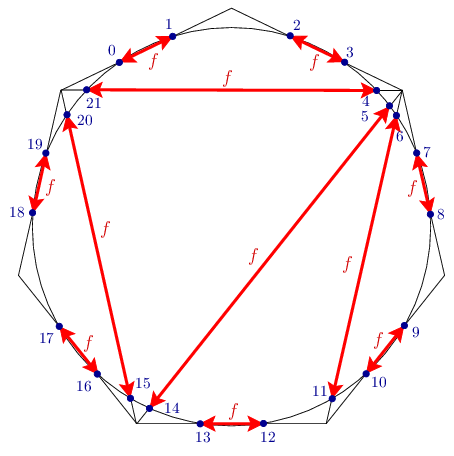
Remark. There exists a function with properties (i--iii) for every $n\equiv 2\pmod4$. For $n=2$ take $f(1)=2$, $f(2)=1$. Here we outline a possible construction for $n\geq 6$.

Let $n=4k+2$, take a regular polygon with $k+2$ sides, and divide it into $k$ triangles with $k-1$ diagonals. Draw a circle that intersects each side and each diagonal twice; altogether we have $4k+2$ intersections. Label the intersection points clockwise around the circle. On every side and diagonal we have two intersections; let $f$ send them to each other.

This function $f$ obviously satisfies properties~(i) and~(ii). For every $x$ we either have $f(x+1)=x$ or the effect of adding 1 and taking $f$ three times is going around the three sides of a triangle, so this function satisfies property~(iii).